인덱스 구조 및 탐색 : 수직적 탐색 과정과 LMC(친절한 SQL 튜닝)
인덱스 구조 및 탐색
DBMS가 발명된지 수 십년이 지났지만, 사실상 현존하는 SQL의 테이블 스캔 방법은 두 가지다.
1. 테이블 전체를 스캔(Full Scan)
2. 인덱스를 사용(Random Access)
이 두 가지 과정에서 당연하게도 인덱스를 사용하는 것이 실제 튜닝을 통해 성능을 개선할 요소가 많다.
FS 자체는 그다지 (물리적으로 개선하는 것이 아니라면) 의미가 없을 것이다.
인덱스 튜닝의 핵심 요소
1. 인덱스 스캔 과정에서 발생하는 비효율을 줄이기 (인덱스 스캔 효율 튜닝)
소량 데이터 검색 시에는 인덱스 자체의 튜닝을 줄이는 것이 중요하다.

예시에서는 복합 인덱스의 순서처럼, 중복도가 낮은 순서대로 정렬하는 것의 예시를 들었다.
이 경우 테이블 내에서 전체 스캔해야 할 내용은 적어지며, 순서에 따라 스캔 효율 자체가 차이가 발생한다.
2. 테이블 접근의 횟수 자체를 줄이기
이는 테이블 조회 IO 자체를 줄이는 것에 가까우며, 인덱스를 사용하여 테이블 접근시 주로 랜덤 엑세스를 사용하기에 '랜덤 액세스 최소화 튜닝' 이라고 한다.
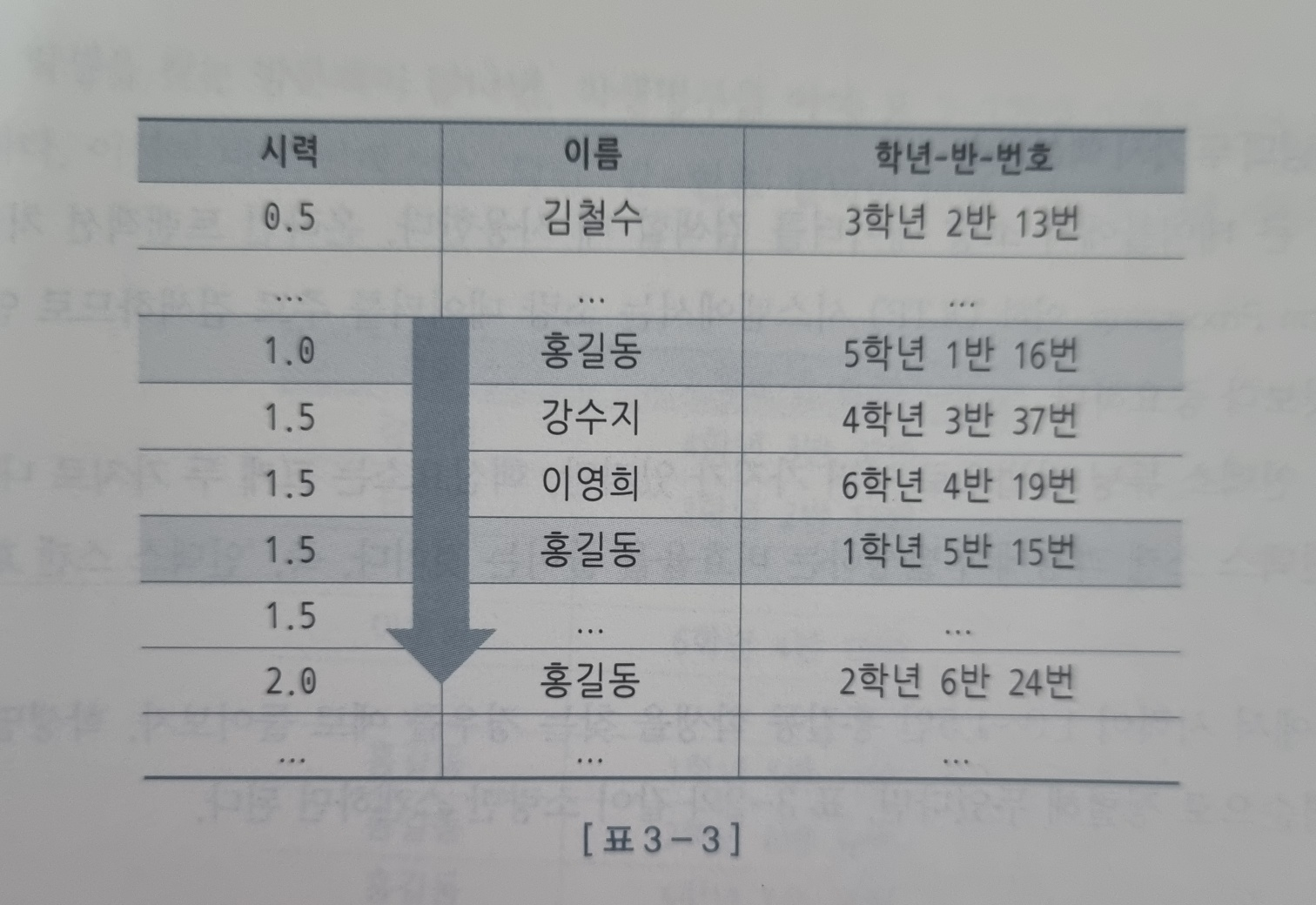
예제의 레코드를 다시 확인해보자.
만일 다음과 같은 결과에서 '시력' 과 '이름' 의 각각 단일 인덱스만 있다면 어떻게 해야 할까?
당연히 이름 순으로(물론 시력이 중복도가 높기에 기본적으로 예시가 조금 애매하긴 하지만) 있는 인덱스를 사용하는 것이 더 높은 효율을 가진다.
이는 실제 데이터가 담겨 있는 테이블을 적게 접근할 수 있는 '이름 순 정렬된 인덱스' 가 더 높은 효율을 가진다.
실제 페이지 블록에 접근하는 IO 엑세스가 적기 때문이다.
이는 '수평적 탐색' 과 연관이 있다.
인덱스를 적절히 활용하여 불필요한 수평적 탐색을 줄이는 것이 테이블 접근 횟수를 줄이는 핵심적인 방법 중 하나이다.
의의
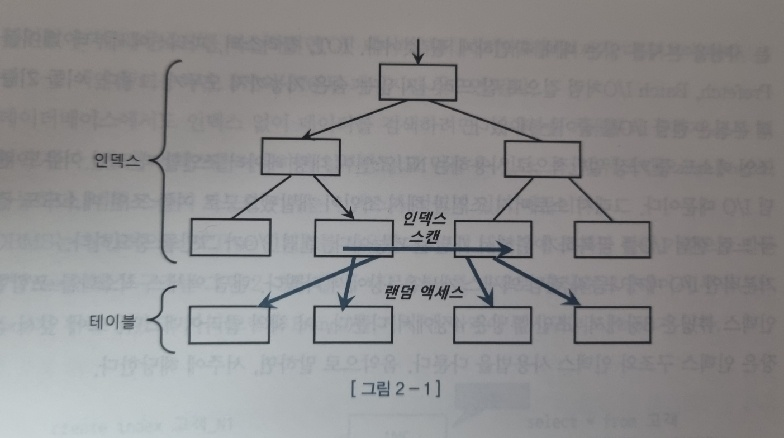
X축을 가로지르는 수평적인 인덱스 스캔을 보다 보면, 여러 페이지 블록을 확인해야 한다는 점 역시 확인할 수 있다.
근본적으로 DBMS의 성능이 느린 이유는 디스크 I/O가 대다수를 차지한다.
물리적 디스크 탐색 기간이 크기 때문이다.
현존하는 DBMS의 많은 기능등은 느린 랜덤 액세스 접근을 개선하기 위해 개발되었다.
두 가지 요소 중 성능 향상에 더 의의가 있는것은 테이블 접근 자체를 줄여 IO를 개선하는 '랜덤 액세스 최소화 튜닝' 이 더 의미가 있다.
이것은 결국 SQL 튜닝의 큰 틀 자체가 '랜덤 I/O를 줄이는 것'을 목표로 한다는 것을 의미한다.
인덱스 구조
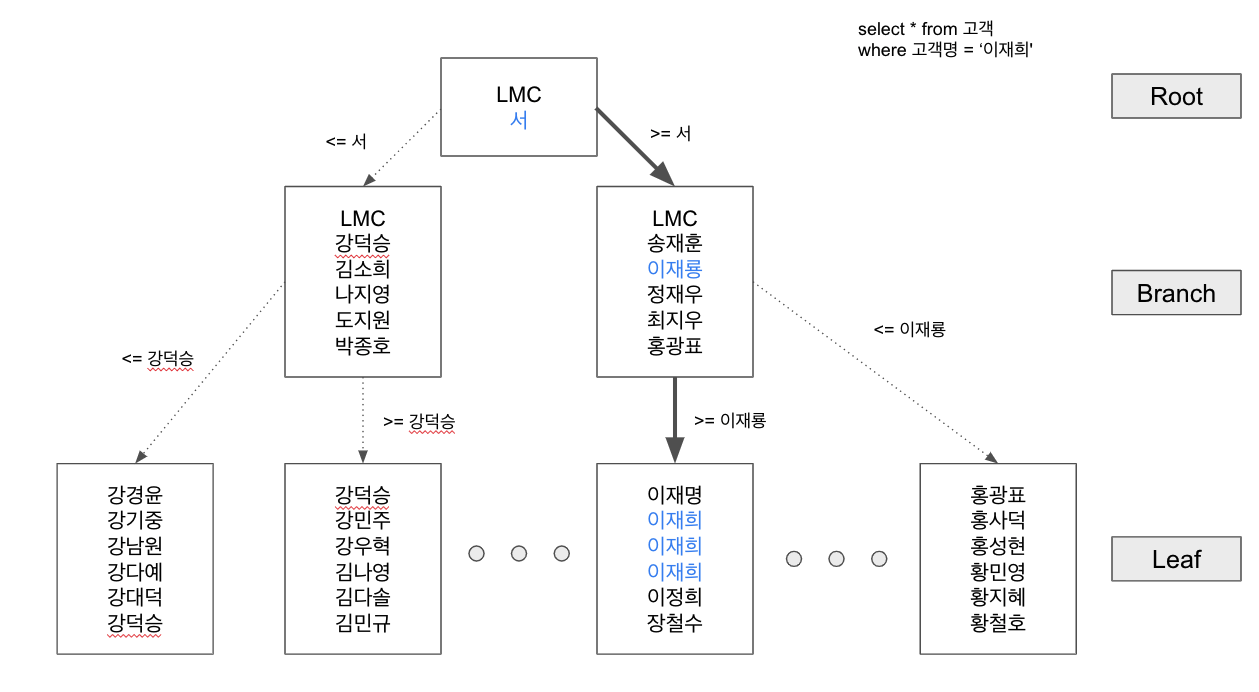
일반적으로 우리가 잘 아는 B-Tree 구조의 예시는 다음과 같다.
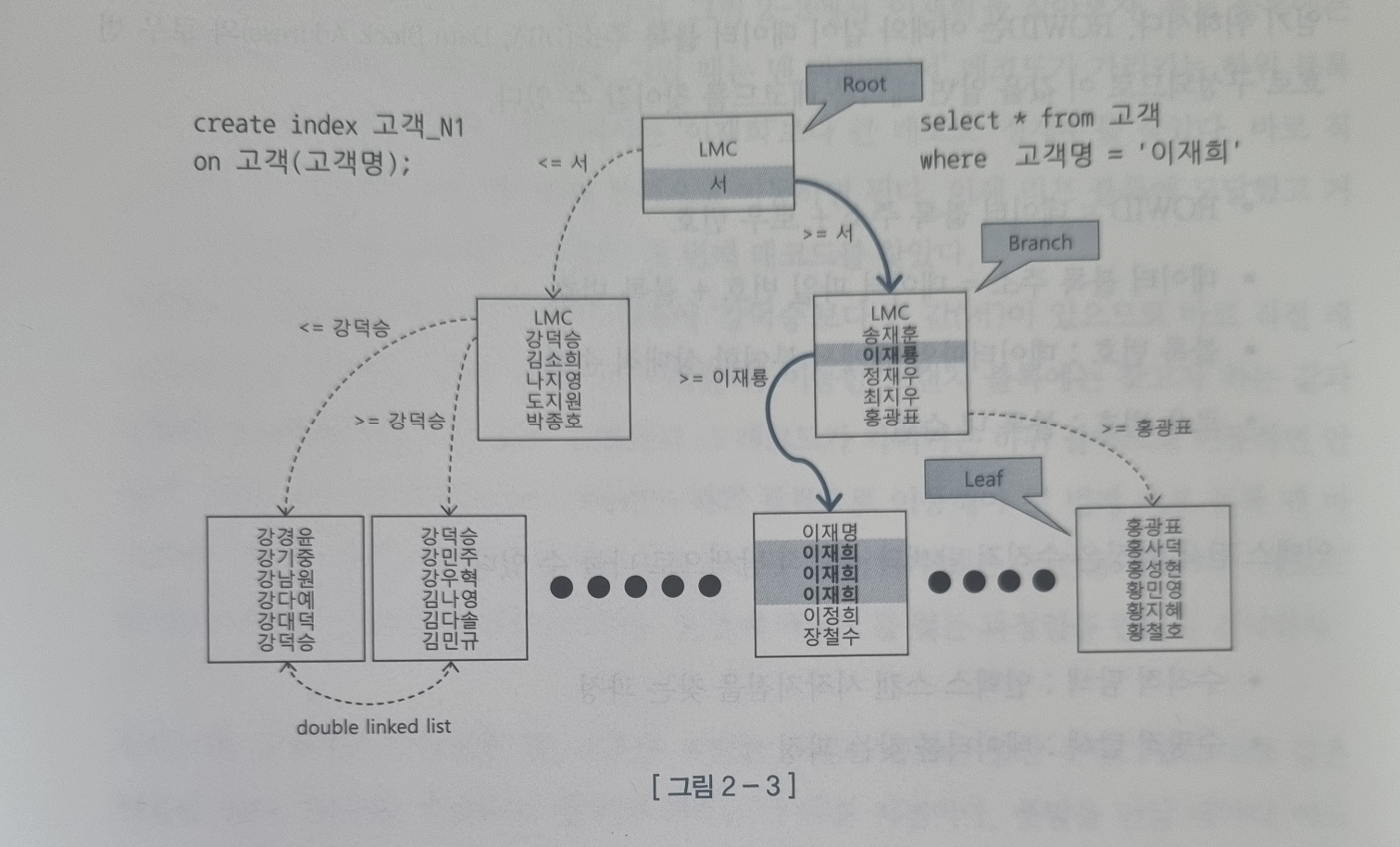
본 그림의 예시 일부를 보면, '이재룡' 의 블록의 하위 리프에는 '이재룡' 보다 크거나 같은(varchar) 노드가 하위에 있음을 확인할 수 있다. 이것은 일반적인 설명이지만, 해당 사진에서 확인해야 할 부분이 있다.
LMC(Leftmost Child)
모든 노드는 LMC를 가지며,
루트와 브랜치(내부) 노드에서 LMC는 키 값이 아닌 자식 노드를 가리키는 포인터로서의 역할을 한다.
B-Tree 내부에서 LMC(Leftmost Child)는 B-Tree 노드의 왼쪽 가장 하위 자식 노드를 의미한다.
LMC는 특정 노드의 하위 노드 중 가장 작은 값을 가진 노드를 가리키며, 특히 트리의 정렬성과 탐색 성능을 보장하는 데 중요한 역할을 한다.
루트와 브랜치 노드의 경우 : LMC는 키 값만 포함하고 실제 데이터는 포함하지 않을 수도 있다.
이 경우 LMC가 가리키는 주소로 찾아간 블록은, 해당 노드의 가장 왼쪽 자식 노드를 가리키는 포인터 역할만 한다. 즉, LMC 자체가 키 값을 가지지 않을 수 있다.
리프 노드의 경우는 데이터를 가지게 된다.
B-Tree의 리프 노드는 일반적으로 실제 데이터를 포함하는 노드로, LMC도 키 값을 가질 수 있다. 리프 노드까지 내려갔을 때 LMC는 가장 작은 값을 포함한 노드가 된다.

https://medium.com/@egorponomarev/b-tree-index-in-postgresql-b4e3ac8ed92f
B-tree index in PostgreSQL
In this post, I will try to explain how the B-tree index of PostgreSQL works.
medium.com
psql에서의 실제 LMC 확인 값 중 일부이다.
이는 추후 수직적 탐색에서 다시 언급한다.
수평적 탐색과 수직적 탐색의 개요
이 내용을 인지한 뒤에는 수평적 탐색과 수직적 탐색에 대한 의미를 어느정도 이해할 수 있었다.
수직적 탐색 : "인덱스 스캔의 시작 지점을 탐색"
수직적 탐색은 트리의 루트에서 리프 노드로 내려가는 과정을 의미한다. 트리 구조의 상위 노드부터 시작해, 조건에 맞는 하위 노드로 내려가면서 원하는 데이터를 포함한 리프 노드를 찾아가는 방식이다.
수평적 탐색 : "해당 지점에서의 목표 데이터를 실제 탐색"
수평적 탐색은 리프 노드의 데이터 블록 안에서 목표 데이터를 찾는 과정을 의미한다. 수직 탐색을 통해 원하는 리프 노드를 찾은 후, 해당 노드에서 원하는 레코드를 찾기 위해 좌우로 이동하며 값을 탐색하는 것이다. 이 과정은 리프 노드 수준에서 발생하는 탐색이므로 "수평적 탐색"이라 불린다.
인덱스 수직적 탐색은 LMC와 밀접한 관련이 있다.
인덱스 스캔의 시작 지점을 탐색, 즉 정렬된 인덱스의 '첫 번째' 레코드를 찾는 과정이다.
쉽게 생각해보자. 기본적으로 트리 구조라고 할 때, 우리는 '가장 위에서부터' 탐색을 시작할 것이다. 그렇다.
인덱스 탐색은 Root Node부터 시작된다.
루트 노드부터 각 브랜치 블록은 전부 '하위 블록에 대한 주소 값' 을 가지며 이는 리프 노드 끝까지 수직적으로 탐색이 가능한 이유이다.
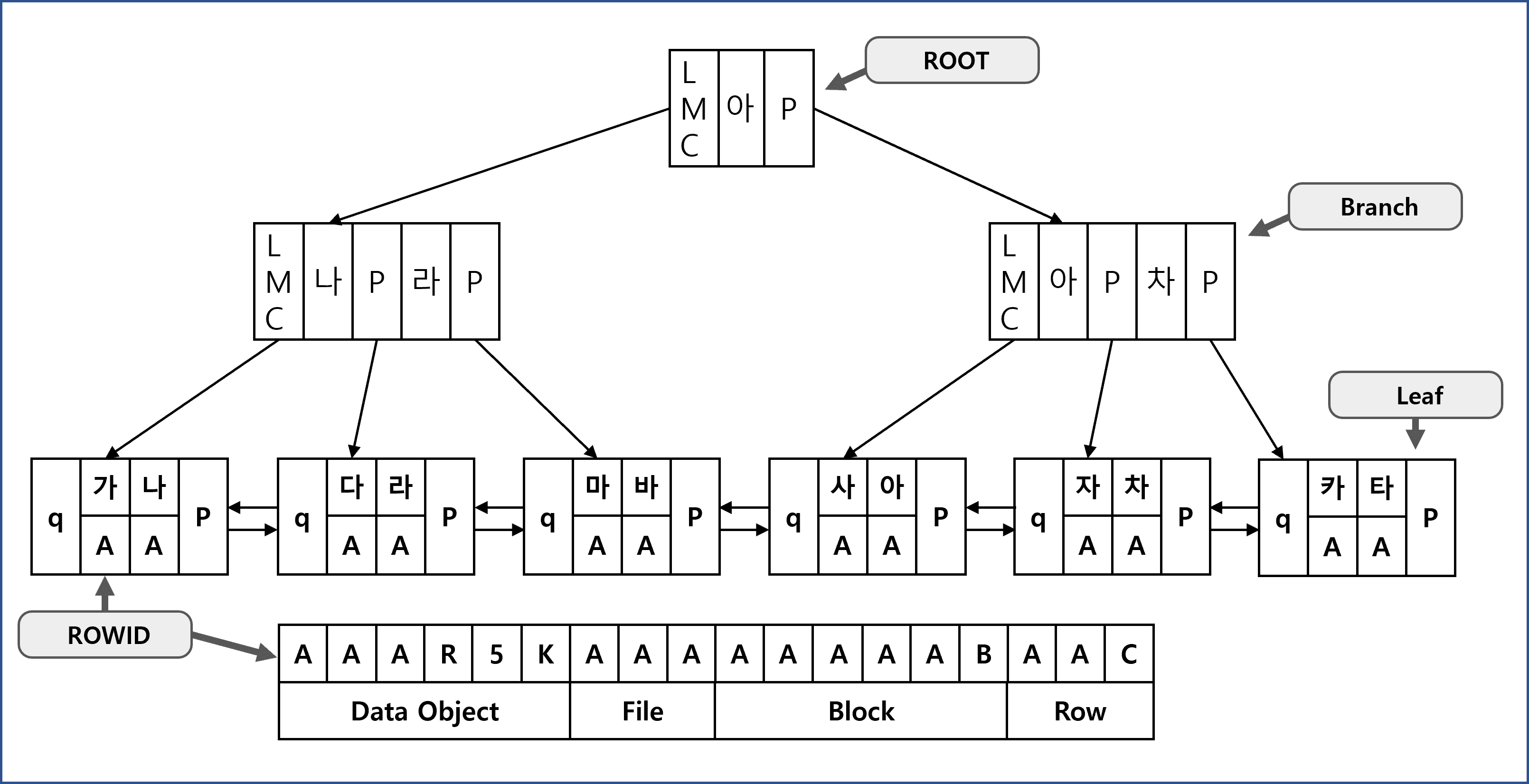
이 구조 덕분에, 트리의 최상단에서 시작하여 LMC를 따라가면 정렬된 인덱스에서 첫 번째 데이터로 빠르게 도달할 수 있다. B-Tree 구조의 특성상 노드들이 항상 키 값 순서대로 정렬되어 있기 때문이다.
이것을 조금 더 다르게 말하자면, 수직적 탐색을 통해 가장 작은 값을 찾고자 할 때는 각 노드에서 LMC만 따라 내려가면 된다는 뜻이다.
수직적 탐색은 '조건을 만족하는 레코드를 찾는 것'이 아니라,
'조건을 만족하는 첫 번째 레코드를 찾는 과정' 임을 기억하자.
최소값을 LMC를 통해 찾는 과정
1. 루트 노드에서 시작
인덱스 스캔은 항상 루트 노드에서 시작하여 필요한 키 값을 찾기 위해 트리 구조를 아래로 내려간다.
2. 각 레벨에서 LMC 선택
가장 작은 값을 찾는 경우에는 각 레벨에서 LMC를 따라가게 된다. 특히 특정 조건에 맞는 최솟값을 찾는 경우에는 루트에서 리프까지 각 노드에서 가장 왼쪽 자식을 따라가며 수직적 탐색이 수행된다.
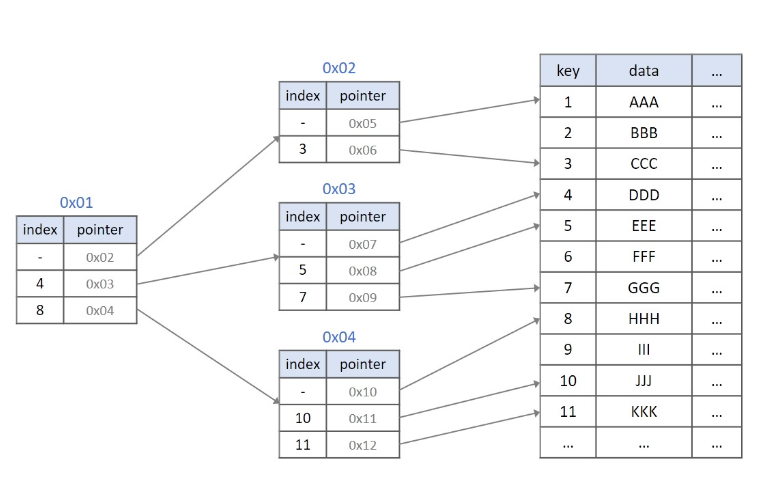
3. 리프 노드 도달
수직적 탐색을 통해 리프 노드에 도달하면, B-Tree 구조에 따라 리프 노드에 저장된 데이터 블록에 접근할 수 있다.
B+Tree의 경우 리프 노드에 실제 데이터 포인터가 존재하므로 바로 데이터를 조회할 수 있으며, B-Tree의 경우 리프 노드로부터 데이터 페이지를 별도로 찾아가게 된다.
4. 정렬된 순서로 데이터 반환
최종적으로 찾은 리프 노드에서 데이터를 반환하거나 추가로 수평 탐색을 통해 인접 데이터를 조회할 수 있다.
최댓값의 경우는 RMC(Rightmost Child)를 따라가는 방식으로 탐색
일반적으로 루트 노드나 특정 상황 등에서 자식 노드의 최소 개수만 가지지 않는다면,
RMC는 모든 내부 노드(비 리프 노드)에서 항상 존재한다.
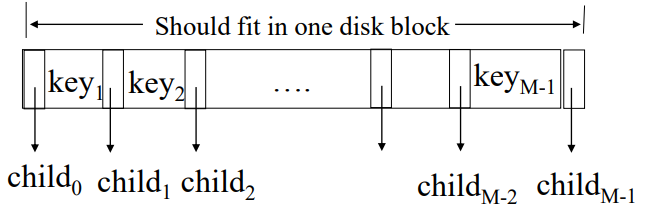
B-Tree는 각 노드가 특정 범위 내의 자식을 가지도록 설계되기 때문에, 대부분의 경우 최우측 자식(RMC)이 없는 상태로는 노드가 구성되지 않는다.
따라서 RMC는 일반적으로 존재하며, LMC의 예시와 같이 트리의 오른쪽 끝까지 내려가면 최댓값에 도달할 수 있다.